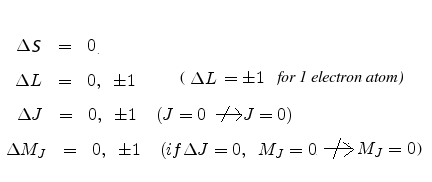Anomalous Zeeman effect

In normal Zeeman effect, we studied the splitting of spectral lines into three components in an one electron atom in the presence of a weak magnetic field. Although not stated explicitly, we had then assumed erroneously that the electron did not have any spin. Actually, normal Zeeman Effect is observed in multi-electron atoms with even number of optically active electrons, the electronic transitions occuring between Singlet states (Total spin quantum number S=0, multiplicity=2S+1=1), as for example between ¹P and ¹S states.

On the other hand when electronic transitions occur in single or multi-electron atoms in the presence of weak magnetic fields between Multiplet states (Total spin quantum number S=1/2, multiplicity=2S+1=2 (Doublet), S=1, multiplicity=2S+1=3 (Triplet) etc), as for example between ²P_3/2 and ²S_1/2 states, we observe many more lines and the effect is called anomalous Zeeman effect. It can be explained through the LS coupling of the individual angular momentum vectors and the behaviour of the resultant total angular momentum vector and the total magnetic dipole moment in the presence of the external magnetic field.

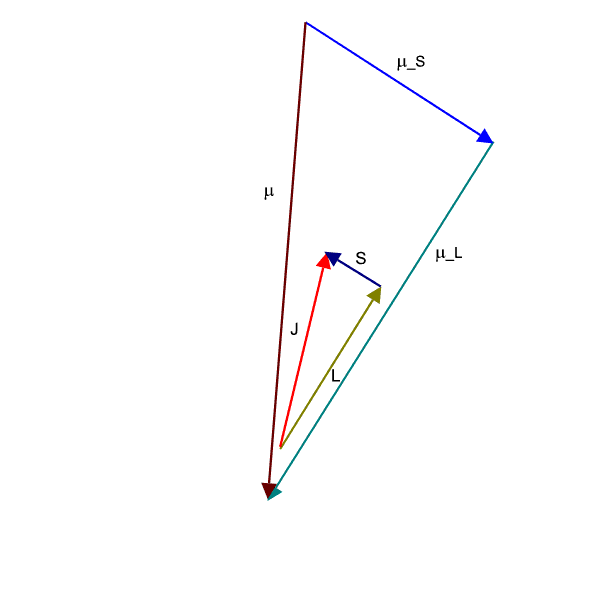
The term 'anomalous' originates from the fact that the total magnetic moment $\bf\mu$ = $\bf\mu_{L}$ + $\bf\mu_{s}$ is not antiparallel (and therefore not collinear) to the total angular momentum ${\bf J=L+S}$. This is because of the gyromagnetic ratio having a value $\ne$1. This again follows from the expressions relating the the orbital magnetic moment and orbital angular momentum ($\mu$ and $\bf L$) and also the spin magnetic moment and spin angular momentum ($\mu_{{s}}^{}$ and $\bf S$). This is best illustrated in a vector diagram as shown below:

In the vector model, the atom obeys LS coupling. The individual orbital and spin angular momenta precess very fast about their respective resultants $\bf L$ and $\bf S$ which in turn precess a little less faster around $\bf J$ which also precess, albeit still less faster, around the external magnetic field $\bf B$.

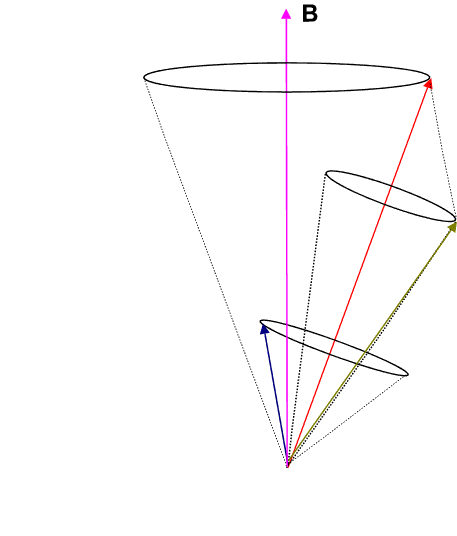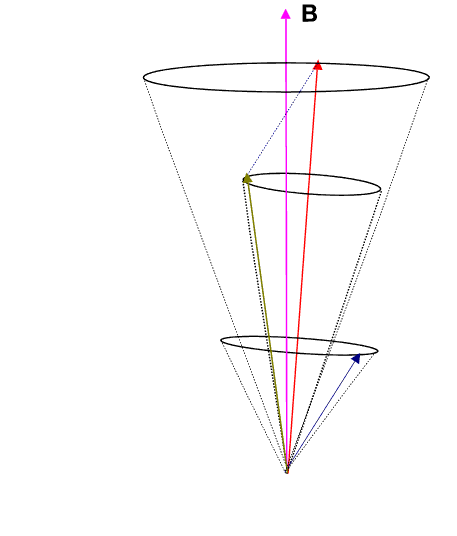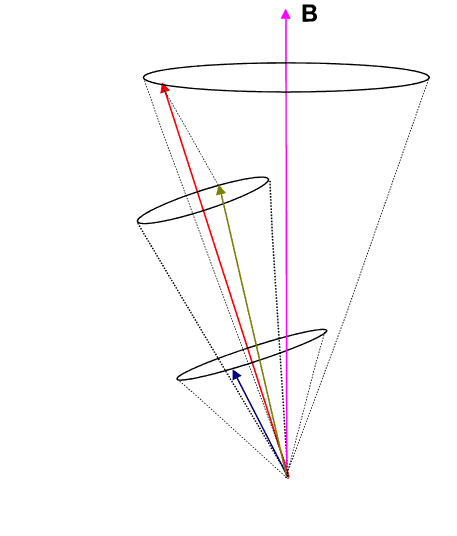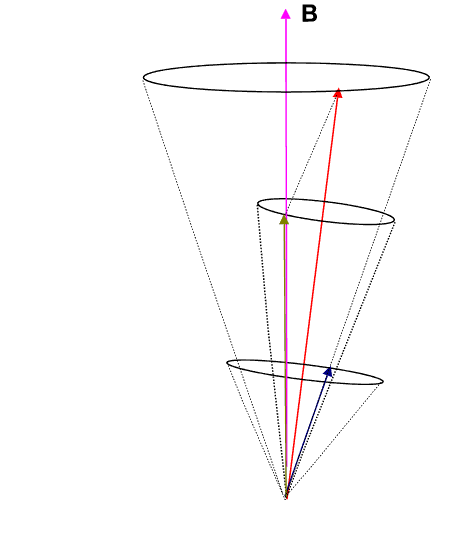
If we employ the vector model as has been done in the animation below, we observe that the $\bf L$ (brownish-yellow) and $\bf S$ (deep-blue) vectors precess about $\bf J$ (red) (due to spin-orbit coupling), which in turn precesses slowly about the external magnetic field $\bf B$ (pink) which lies parallel to the z-axis.

Due to the precessing of the angular momentum vectors $\bf L$ and $\bf S$ about the resultant $\bf J$, the magnetic moment vectors $\bf\mu_{L}$, $\bf\mu_{s}$ as well as $\bf\mu$ precess about $\bf J$. Only the component of $\bf\mu$ parallel to $\bf J$, viz., $\bf\mu_{J}$ survives as all the components of perpendicular to $\bf\mu$ average out to zero. Thus the splitting of levels depends only on $\bf\mu_{J}$ (which is antiparallel to $\bf J$ and like $\bf J$ precesses very slowly around the external magnetic field $\bf B$). The corresponding potential energy of interaction is given by

$$\begin{eqnarray*} \Delta E & = & -\mathbf{\mu_{J}}\cdot \mathbf{B} \\ & = &... ... & \frac{e}{2m} g J_{z} B \\ & = & \frac{e}{2m} g M_{j} \hbar B \end{eqnarray*}$$

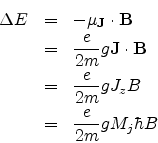
where g is called the Lande g-factor and is given by

$$\begin{eqnarray*} g & = & 1+ \frac{J(J+1)-L(L+1)-S(S+1)}{2J(J+1)} \end{eqnarray*}$$ Thus each energy level splits into 2J + 1 levels, since M_J=-J to +J in integral steps.

It is very important to note that for singlet states the spin quantum number S=0 so that J=L and the Lande g-factor becomes equal to the gyromagnetic ratio=2. Hence the above formulation reduces to that of the normal Zeeman effect which was explained earlier in terms of only the orbital angular momentum and its associated magnetic moment.

The emission spectrum of the atom placed in the external magnetic field $\bf B$ will show additional lines apart from the original line which corresponds to the situation when $\bf B$=0. The pertinent selection rules for electric dipole transitions are

For example, in a weak magnetic field (less than 1 Tesla) the fine-structure splitted sodium doublet due to transitions between the levels ²P_3/2 to ²S_1/2 and ²P_1/2 and ²S_1/2 are further Zeeman splitted into four and six lines respectively.