Angular momentum and its quantization

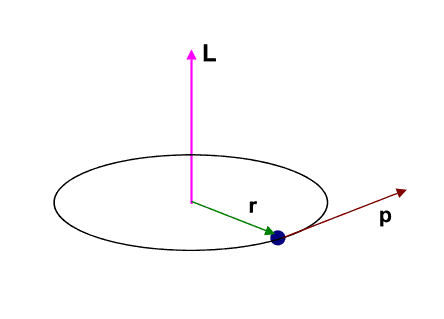
The angular momentum L, as we know from classical mechanics, is given by

$$\mathbf{L} = \mathbf{r}\times\mathbf{p} = \left \vert \... ... & y & z \\ p_{x} & p_{y} & p_{z} \end{array}\right \vert$$

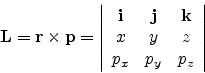
x, y, z being the position coordinates and p_x, p_y, p_z being the corresponding linear momenta.

The three angular momentum components are therefore

$$\begin{eqnarray*} L_{x} & = & yp_{z}-zp_{x} \\ L_{y} & = & zp_{x}-xp_{z} \\ L_{z} & = & xp_{y}-yp_{x} \end{eqnarray*}$$

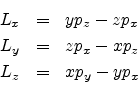
In quantum mechanics, we work with the corresponding operators, obtained in the position representation by replacing the position coordinates q_i by themselves and the momentum coordinates p_i by - i$\hbar$${\frac{{\partial}}{{\partial q_{i}}}}$ as follows

$$\begin{eqnarray*} L_{x} & = & -i\hbar (y\frac{\partial}{\partial z} - z \frac... ...(x\frac{\partial}{\partial y} - y \frac{\partial}{\partial x}) \end{eqnarray*}$$

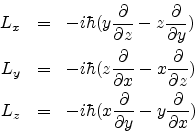
We already know what is meant by commutation relations for operators. Let us check out the commutation relations for the angular momentum operators:

$$\begin{eqnarray*} \left[ L_{x},L_{y} \right] & = & i\hbar L_{z} \\ \left[ L... ...i\hbar L_{x} \\ \left[ L_{z},L_{x} \right] & = & i\hbar L_{y} \end{eqnarray*}$$

It may also be shown that $$\begin{eqnarray*} \left[ L^{2},L_{x} \right] & = & 0 \\ \left[ L^{2},L_{y} \right] & = & 0 \\ \left[ L^{2},L_{z} \right] & = & 0 \end{eqnarray*}$$ where $$\begin{eqnarray*} L^{2}= L_{x}^{2}+L_{y}^{2}+L_{z}^{2} \end{eqnarray*}$$

We have discussed earlier that any pair of complementary observables whose operators do not commute cannot be determined simultaneously. Hence from the above commutation relations we find that only one component of the angular momentum can be specified precisely. As per convention, we take this component to be L_z, but we could as well have chosen L_x or L_y.

Notice also that L² commutes with each of the components, hence the magnitude of the angular momentum |$\bf L$| can be specified simultaneously with each of its components.

Thus the two fundamental observables are L² and L_z.

We would soon encounter another angular momentum observable called spin, denoted by S. Hence it would be better if we use a general notation for angular momentum, viz., J. The two fundamental observables, in this notation, are J² and J_z

Since J² and J_z commute, they have the same eigenstate or eigenfunction which is represented in terms of two quantum numbers j and m_j as follows:

$$\begin{eqnarray*} J^{2} \vert j,m_{j}> & = & j(j+1)\hbar^{2}\vert j,m_{j}> \\ J_{z} \vert j,m_{j}> & = & m_{j}\hbar \vert j,m_{j}> \end{eqnarray*}$$

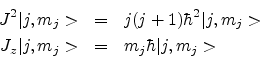
The corresponding eigenvalues are j(j + 1) and m_j. j can have integer or half-integer values and m_j = - j... + j in integral steps.

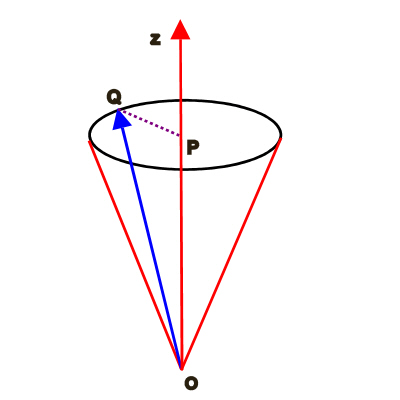
OQ = |$\bf J$| = $\sqrt{{j(j+1)}}$$\hbar$ and OP = J_z = m_j$\hbar$. Note that if J_z is specified or fixed we may simultaneously specify only |$\bf J$|. The direction of $\bf J$ is arbitrary. In the vector model of angular momentum shown through the figure above, $\bf J$ may be represented by the sides of a cone ( any one among the many shortest lines joining the vertex of the cone to the periphery of the bottom of the cone, but subject to the quantization condition on J_z), the height of the cone being fixed at J_z. In the process J_x and J_y also become arbitrary.