* Now we shall introduce ourselves to the vector form of the Bragg equation, viz. ![]() through a geometrical construction called the
Ewald sphere.
through a geometrical construction called the
Ewald sphere.
Note, k is the incident wave vector on the set of parallel planes of the crystal lattice and G is the reciprocal lattice vector which would make the occurance of a Bragg diffracion maxima possible.
Use the button(s) at the bottom of the box to have a pictorial understanding of the steps.
The sequence of steps is explained in some more detail below:
(i) We start with a given set of reciprocal lattice points.
(ii) We draw a vector
AO in the direction of the incident X-ray so that the length of the vector
BO = (AO/2) is
|BO|= (2![]() /
/![]() ).
). ![]() is the wavelength of the incident radiation. Therefore
BO is nothing but the incident wave vector
k. Let us consider the terminal point of
k i.e.O as the origin of the reciprocal lattice space.
is the wavelength of the incident radiation. Therefore
BO is nothing but the incident wave vector
k. Let us consider the terminal point of
k i.e.O as the origin of the reciprocal lattice space.
(iii) Next we draw a circle with B as center and BO as radius. Let this circle pass through a reciprocal lattice point C.
(iv) We join OC and BC.
OC must therefore represent a reciprocal lattice vector
G = ![]() which again must be perpendicular to the (hkl) planes of the direct lattice.
which again must be perpendicular to the (hkl) planes of the direct lattice.
(v) From the geometry it is evident that AC or equivalently EH represents the above (hkl) planes since AC is perpendicular to OC and EH is parallel to AC
We may then think of
AB = BO as the wave vector
k incident on the (hkl) plane EH of the direct lattice and
BC as the resulting specular reflected wave vector
k/ at the point B.
k/ = k + G
Let
k =|k| and
k/ =|k/|.
Since AB=BC, therefore
k = k/ = (2![]() /
/![]() ).
).
* So we may write
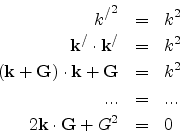 which is nothing but the vector form of Bragg's equation. The last equation can be equivalently expressed as
which is nothing but the vector form of Bragg's equation. The last equation can be equivalently expressed as
![]()
* Extrapolating the construction to three-dimensions we obtain the Ewald's sphere. We therefore observe that when a sphere is drawn on a reciprocal lattice with radius equal to the magnitude of the wave vector, i.e.,
k = (2![]() /
/![]() ) and centred at the origin of the wave vector
k, and if it intercepts a point in the reciprocal lattice, then Bragg's law is found to be satisfied. The sphere is then called the Ewald's sphere.
) and centred at the origin of the wave vector
k, and if it intercepts a point in the reciprocal lattice, then Bragg's law is found to be satisfied. The sphere is then called the Ewald's sphere.